Figure 1: Diagram of Common Mode Current in a Dipole Transformed into a Model Representation.
At DC the current in a wire has a uniform current density. That means that the current in the wire is equally distributed in the wire. If you could plot the current, as it would appear from looking at the wire, end on, it would appear as a circle of equal density. AC current density is different. As the frequency is increased, the current density tends to be greater at the surface of the wire. Looking at the wire, end on, the current now appears as a donut with a hole in the center. But this is a fuzzy donut. That is to say the edge of the donut in the center does not have a sharp edge but disappears gradually into a hole. When people talk of skin depth, they mean the depth of penetration where the current density is e^-d times the current density at the surface of the conductor where e = 2.718... and d = the number of skin depths.. If d = 1, then that is one skin depth, and the current density is e^-1 or 37 percent of the current density at the surface. The skin depth of copper at 160 meters is about 0.002 inches. So, if you look at the current density at a depth of 0.01 that is 5 skin depths or e^-5 = 0.007 which is less than 1% of the current density at the surface.
Figure 1: Diagram of Common Mode Current in a Dipole
Transformed into a Model Representation.
One could say that at this point we have a tripole instead of a dipole due to this third wire. Please note that the velocity factor of the coax affects the length of the transmission line part of the coax but not the length of the third wire part of the coax. For example, the velocity factor of a typical RG-58 coaxial cable is 0.67. It has a vinyl jacket that has a velocity factor of 0.95. Therefore when you figure the electrical length of the coax, you must use 0.67 for the transmission line part and 0.95 for the outside shield.
EZNEC allows us to model this radiating feed line using the transformation shown in Figure 1. I set the power to 1500 watts and placed the dipole over perfect ground in order to best illustrate the common mode effects. Figure 2 shows the dipole model in an X-Y-Z Cartesian plane. The generator is at the midpoint between the two legs of the dipole labeled 1 and 2. The outside of the shield is represented by the vertical wire labeled 3. The red, curved line represents the current distribution along the wires. A load is placed at the top of the vertical wire. This load will represent our balun later on. Initially the load is set to 0 + J0 so it has no effect.
Figure 2: EZNEC Model of a 1/2 Wave Dipole ~ 1/2
WL Over Perfect Ground with Feed Line Not Grounded and Driven with
1500 Watts.
Figure 2 shows that the current imbalance in the two dipole legs and the feed line current are minimum. The current distribution along the two legs of the dipole, as indicated by the red curve, is exactly what you would expect. It reaches a maximum at the center of the dipole and is minimum at the two ends. The voltage distribution is just the opposite, reaching a maximum at the two ends and going through a minimum at the center. The feed point impedance, also, looks correct for a dipole in this configuration. Now we will ground the feed line and see what happens. Figure 3 shows the result of grounding the feed line at the bottom. In a real situation, this grounding might be a ground strap tied to the shield of the coax as it enters the shack, a ground strap tied to the tuner, amplifier, or transceiver or the ground wire on the AC receptacle in the shack. In fact, since the length is important, you must know what it is.
Figure 3: EZNEC Model of a 1/2 Wave Dipole ~ 1/2
wl Over Perfect Ground with ~1/2 wl Feed Line Grounded and Driven
with 1500 Watts.
You can see from Figure 3 that the current distribution and the feed point impedance are very different from Figure 2. In fact, if we subtract the 5.9 Amp current in the outside shield of the feed line from the 6.4 Amp current in dipole leg 1, you get the 0.5 Amp current left in dipole leg 2. The current that should be flowing in dipole leg 2 is now flowing in the outside shield of the feed line. Not only is the current distribution altered, but the feed point impedance looks more like a vertical than a dipole. In fact, you could view this as an inverted vertical with one radial. This is not a good situation. Not only does this alter the radiation pattern that we expect, it causes radiation in the shack. Remember that the ground connection at the bottom end of wire 3 could be very close to equipment in the house. It is as we have moved the ground up to the leg of the dipole and provided a low impedance path for the current to flow.
I have chosen a feed line length that maximizes the feed line radiation for demonstration purposes. If you chose the feed line to be close to 1/4 wl and leave the end open instead of grounded, feed line currents will also flow on the outside of the coax. The current distribution on the feed line will look like just the upper half of the distribution on wire 3 in Figure 3. The feed line lengths that maximize common mode currents are odd multiples of 1/4 wl and multiples of 1/2 wl. In order to determine how far you have to stay away from these critical lengths with a grounded feed line end, I used EZNEC to determine the currents for various lengths of grounded feed lines. Figure 4 shows the results of those calculations.
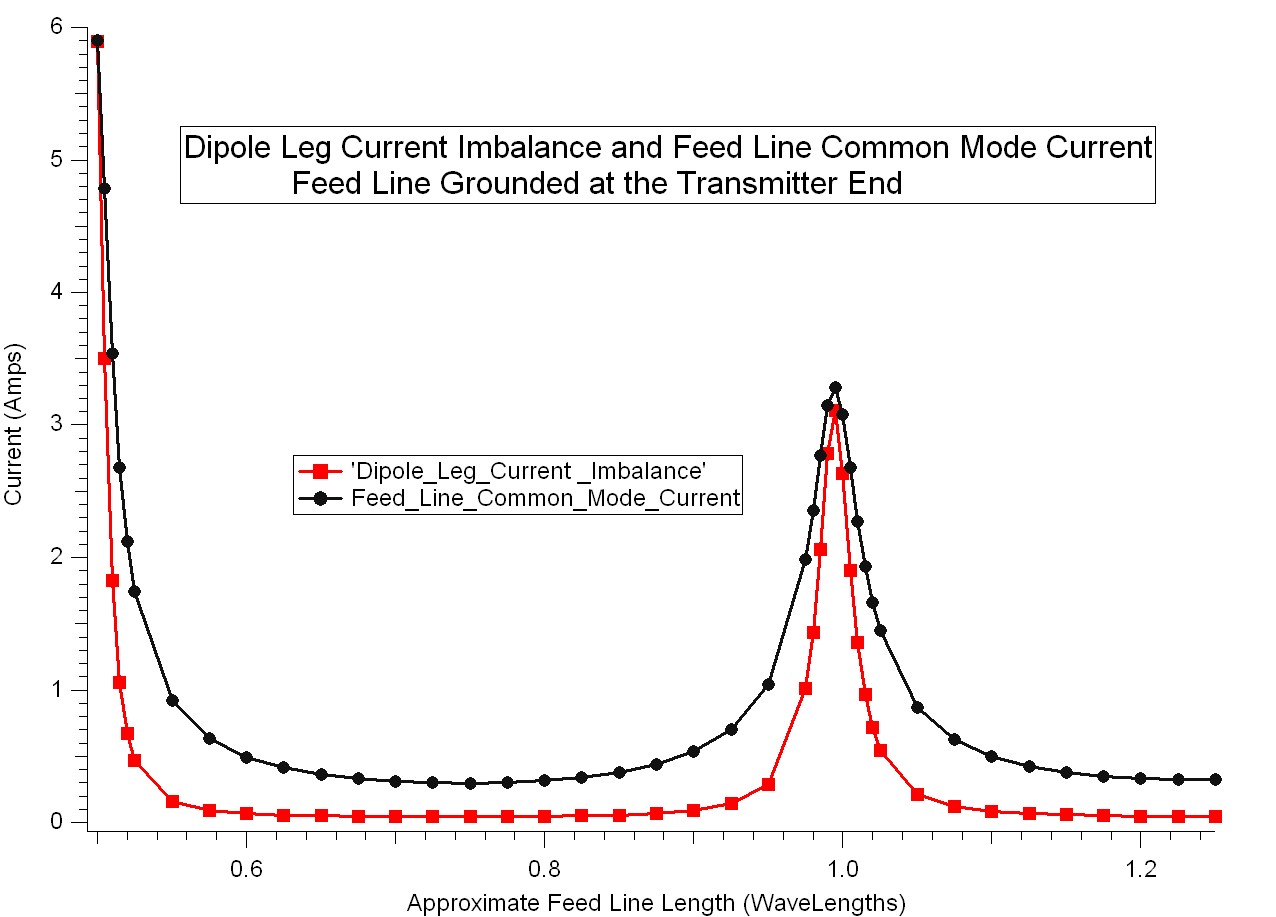
Figure 4: Dipole Leg Current Imbalance and Feed Line Common Mode Current vs Length of a Grounded Feed Line. 1500 Watts Drive Power
You can see from Figure 4 that the dipole leg current imbalance and the feed line common mode current are correlated, which is exactly what you would expect. Also, you can see that if you stay at least 1/8wl away from multiples of 1/2 wl feed line lengths, the imbalance and common mode problem is greatly mitigated. It is also interesting to note that the problem diminishes as the feed line gets longer. I thought this was due to loss, but I ran the model again with zero loss and this phenomenon still occurs.
Altering the feed line length will change the impedance that the transmitter sees in the shack if the antenna feed point impedance does not exactly match the transmission line characteristic impedance. But if you are operating close to a length that causes high common mode currents, the feed point of the antenna is actually changed. Now you see the impedance being transformed as a function of the feed line length, when measured in the shack, and the feed point impedance at the antenna is being actually being changed as a function of feed line length. This becomes a measurement nightmare if you are trying to make antenna impedance measurements from within the shack.
In order to illustrate this further, the same dipole that is shown in Figure 3 was modeled exactly the same but with 1/8 wl of feed line added. The results are shown in Figure 5.
Figure 5: EZNEC Model of a 1/2 Wave Dipole ~ 1/2 wl Over Perfect Ground with ~5/8 wl Feed Line Grounded and Driven with 1500 Watts.
You can see that by just adding 1/8 wl of feed line, the dipole leg current imbalance is corrected, the common mode current in the feed line is reduced, and the feed point impedance of the antenna is restored to a reasonable value.
Selecting the right feed line length may not be the easiest way to get rid of common mode feed line currents. We may be operating from an upstairs apartment where a good ground is not easily obtained. Our feed line may feed multiple antennas where the feed line length would have to vary with frequency. The common mode choke sometimes called a choke balun is the answer. Common mode chokes come in a variety of flavors. Essentially a choke balun is a current balun, and may be as simple as several turns of feed line wound in a nice solenoid coil about 6 inches in diameter. I have used these since the 1960's on antennas for 14 MHz and above. These chokes have the advantage that the impedance is entirely reactive and thus heating is not an issue, since there is no lossy resistive part of the impedance. The disadvantage of this kind of choke is getting a high enough impedance at the lower frequencies. Ferrite cores and rods have also been used for many years. Unfortunately, they have been used in voltage balun applications where the whole transmitter power passes through the windings. Overheating and core saturation in this application have given the ferrite a bad reputation. When you use a ferrite in a common mode application, the stresses on the core are much less, but you still have to be careful! We will discuss some of these precautions later, but right now let's just see what a common mode choke will do. In a previous toroid article, I discussed a common mode choke consisting of 15 turns of RG-58 coax wound on an FT-240-43 core. This has an impedance of 5000 - J5000 at 7 Mhz. If we create a load of this value at the upper end of wire 3 in our model shown in Figure 3, we get the results shown in Figure 6.
Figure 6: EZNEC Model of a 1/2 Wave Dipole ~ 1/2 wl Over Perfect Ground with ~1/2 wl Feed Line Grounded and Driven with 1500 Watts. A Common Mode choke Consisting of 15 turns of RG-58 on FT-240-43 Core is Employed. Z = 5000 - J5000. 1.33 Watts (0.004 db) is Lost in the Core with 1500 Watts Drive.
You will notice that the common mode choke balances the dipole leg currents very well, the feed line common mode current is greatly reduced, and the feed point impedance is correct. Furthermore, the power lost in the choke is negligible even at maximum drive power. You might notice that the reactive part of the impedance is negative which is capacitive. This occurs because the self resonant point of the choke is below 7 MHz. But this doesn't matter as long as the magnitude of the impedance is sufficiently high and the resistive part of the impedance doesn't dissipate too much power.
I have always heard that a voltage balun does not work well when the SWR is high. But what about the common mode choke which is a current balun? How does it do when the SWR is high? With EZNEC this is easy to evaluate. I just changed the frequency from 7 MHz to 6 MHz and then to 8 MHz. The choke impedance magnitude does not vary much over this range, so I left the choke impedance at 5000 - J5000 for these calculations. If you use the actual values, the numbers only change a bit. The object of this test is to show that high SWR does increase the stress on the choke. Table 1 below shows the results.
| Frequency (MHz) | Impedance (Ohms) | SWR | Dipole Leg 1 Imax (A) | Dipole Leg 2 Imax (A) | Feed Line Imax (A) | Loss in Choke (Watts) | Loss in Choke (db) |
| 7 | 68 - J0.6 | 1.35 : 1 | 4.7 | 4.7 | 0.017 | 1.3 | 0.004 |
| 6 | 54 - J236 | 22 : 1 | 5.3 | 5.2 | 0.066 | 20 | 0.058 |
| 8 | 96 + J257 | 16 : 1 | 4.0 | 4.0 | 0.072 | 16.5 | 0.048 |
Although high SWR does stress the choke, an FT-240 core is probably sufficiently large to take it, especially if you take into account a less than 100% duty cycle encountered in most amateur operations. In fact, the SWR's shown here are extreme. Under normal SWR conditions, the choke probably could handle the stress without any trouble whatsoever.
What about ferrite beads? Again referring to the toroid article, Figure 11 shows 7 ferrite beads of the FB-1020-43 variety yielding a 7 MHz impedance of 300 + J500. Table 2 shows the results of various numbers of these beads slipped over the coax at the feed point.
Table 2: FT-1020-43 Ferrite Bead Choke Balun Chart
| Number of Beads | Zbead @ 7 MHz | Zfeedpoint | Dipole Leg 1 Imax (A) | Dipole Leg 2 Imax (A) | Feed Line Imax (A) | Loss in Choke (Watts) | Loss in Choke (db) |
| 1 | 45 + J112 | 64 + J4.8 | 4.8 | 4.4 | 0.893 | 35.9 | 0.11 |
| 4 | 205 + J308 | 66 + J1.2 | 4.8 | 4.6 | 0.3 | 18.8 | 0.06 |
| 7 | 500 + J300 | 69 + J0.6 | 4.7 | 4.6 | 0.195 | 11.4 | 0.03 |
It is evident from this chart that you can easily overstress a single bead by not placing enough beads on the feed line. Not only is the power that needs to be disspated more, but the suface area of a single bead is smaller than the surface area of several beads. It is like placing a bunch of resistors in series to increase the power disspation capability.
Now that we have established that these common mode currents on the feed line are flowing, let's see what it does to our pattern. We normally are not too concerned about our dipole patterns unless we have the dipole mounted high and in the clear. But the directional antenna is a different matter. We have probably put a lot of effort and money to establish a radiation pattern that has good gain and front-to-back ratio. We don't want that destroyed by feed line radiation, that can upset the pattern of a directional array by radiating itself, or by upsetting the current distribution in the elements that will alter both gain and front-to-back ratio. But how bad is it? I modeled a 3 element Yagi to test this. No particular effort was made to optimize either gain or front-to-back ratio.Figure 7 shows the pattern when the feed line is exactly vertical beneath the Yagi.
Figure 7: Feed Line Common Mode Current Effects on a 3-Element Yagi with a Grounded, ~1/2 wl, Vertical Feed Line Beneath the Yagi.
When you extend the feed line so that it is not vertical, but partially horizontal beneath the Yagi, the effects are even more extreme. Figure 8 shows these effects.
Figure 8: Feed Line Common Mode Current Effects on a 3-Element Yagi with a Grounded, ~1/2 wl, Slanted Feed Line Beneath the Yagi.
The Yagi plot with the balun in Figure 8 looks different than the one in Figure 7 because I lowered the antenna so I could slant the feed line and still reach ground. Nevertheless, the important factor to note is the distortion in the pattern from not having the common mode feed line choke.
What about radiation from the antenna onto the feed line? Common sense tells us that common mode current on the feed line should be lower if the feed line leaves the antenna at a right angle. But, does the choke balun mitigate this type of common mode current? In order to test this, I placed the FT-240-43 choke balun on the feed line model shown in Figure 5. I then rotated the feed line so that it was under Leg 1 of the dipole and then under leg 2 of the dipole instead of being at a right angle to the dipole. Table 3 shows the results of this test.
Table 3: Effects of Feed Line Position on Feed Line Common Mode Current and Choke Stress
| Feed Line Position | Impedance (ohms) | Dipole Leg 1 Imax (A) | Dipole Leg 2 Imax (A) | Feed Line Imax (A) | Loss in Choke (Watts) | Loss in Choke (db) |
| At Right Angle | 68 - J0.64 | 4.7 | 4.7 | 0.03 | 1.45 | 0.004 |
| Under Leg 1 | 76 + J1.6 | 4.4 | 4.4 | 0.81 | 13.7 | 0.04 |
| Under Leg 2 | 67 + J2.5 | 4.7 | 4.7 | 0.85 | 5.7 | 0.016 |
It is apparent from Table 3 that the position of the feed line does make a difference on the amount of feed line common mode current, feed point impedance, and balun stress. Also, it is apparent that feed line common mode current has three sources: 1) Feed line length, 2) Feed line position, and 3) Feed line termination. Also, the balun cannot eliminate that part of the feed line common mode current that is the result of the antenna radiation.
Since this coaxial skin effect causes a third wire to be connected to a dipole, I kept trying to put it to some good use. I travel a lot and sometimes run my ham station in rooms that have balconies. I have been known to stick one end of a fiberglass pole out from the balcony with a counterpoise inside the room. This has the disadvantage of half the antenna being in the room and the high current part of the antenna being near the building. After thinking about this for a while, the antenna shown in Figure 9 occurred to me.
Figure 9: 20 Meter End Connected, Center Fed Balcony Antenna Made From RG-58 Coax.
This antenna makes use of the 3 wire effect caused by the skin effect on the shield of a coaxial cable. I have tried antennas like this in the vertical configuration with the shield folded back on itself, but they never seemed to work quite right. Now I know why! First of all the, there is no need to fold the shield back. The skin effect will isolate the inside from the outside. Also, a trap is needed to "stop" the outer shield at the 1/4 wl point. Since this is a high impedance point anyway, the impedance of the trap needs to be very high at the operating frequency. Figure 10 shows the EZNEC model of the balcony antenna.
Figure 10: EZNEC Model of Balcony Antenna
Theoretically, this antenna should work. If you suspend it over the balcony on a fiberglass pole, all the radiation is outside of the building and the radiation pattern is away from the building. I run a 600 watt, home-brew, solid state amplifier when I travel. If I operate SSB, then the trap will dissipate 8 watts when I transmit. It will dissipate about 19 watts on CW. The mass of the trap should be able to handle this. The trap was calculated on the basis of an unloaded Q of 300 for the coiled feed line. This may be optimistic. If Qu is lower than 300, the trap losses will go up.
I decided to build this antenna to see if it would really work. Figures 11 and 12 show the finished product.
Figure 11: Two Ends of the Balcony Antenna Showing the Trap and the Center Conductor of the Antenna.
Figure 12: Balcony Antenna in Position for Testing. SteppIR Antenna is Shown Above.
The antenna was built by taking about 40 feet of RG-58 coax and wrapping 14 turns around a thin wall, 1 inch pvc pipe. A 50 pF, 15 kV, NPO capacitor fits inside the pipe and is connected from shield to shield on the coiled RG-58. The coax extends for 17 feet and then the center conductor extends another 17 feet beyond that. The antenna was tested on 20 meters between Boulder, CO and Madison, WI and Boulder and Arlington, VA against the 3 element SteppIR shown in figure 12. The Yagi is at 40 feet. One end of the balcony antenna is at 35 feet and the other end is at 15 feet. Two people in Madison showed 5 db difference while one showed no difference. The person in Arlington showed 20 db difference. In order to insure that the dipole was not coupling into the Yagi and giving it an unfair advantage, I modeled them both together as they appear in Figure 12. There was minimum interaction between the two. In fact the Yagi reduced the gain of the dipole by 1 db, and the effect of the dipole on the yagi was less than 0.2 db. This is not an exhaustive test by any means, but the balcony antenna at least acts as an antenna and proves the concept.
Conclusions
The skin effect that forces RF current to the outside of a conductor causes a dipole fed with coaxial cable to become a tripole. This third wire of the antenna system can cause RFI in the shack and upset the radiation pattern of the antenna. Careful selection of the feed line length can mitigate this effect. Using a choke balun can also mitigate this effect making the feed line length less critical. However, care must be exercised when constructing the choke balun in order to prevent excessive dissipation in the core if a ferrite is used. Finally, this tripole effect can be put to good use in the construction of a balcony antenna that is center fed from the end.
I hope this analysis has been as instructive for you as it was for me!